[latexpage]
Sebelum melakukan regression analysis, perlu mempertimbangkan regression yang akan digunakan. Regression assumptions dapat dibagi dalam 5 kategori:
Linearity
Disebut linear regression, regresi paling sederhana yang menunjukan hubungan antara variable. Disebut linear karena hubungan antar variablenya adalah linear.
$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$
Untuk memeriksa apakah hubungan antara variable adalah linear, dapat dilakukan ploting variable independent x1 terhadap variable dependent y. Jika hasil plotting menunjukan suatu garis lurus, maka linear regression dapat digunakan.
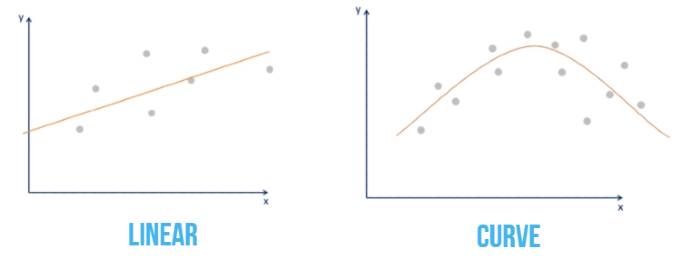
Namun jika hasil plotting tidak menunjukan garis lurus, misalnya curve, ada beberapa pendekatan:
- Gunakan Non Linear Regression.
- Transform data menggunakan exponential transformation.
- Transform data menggunakan logaritma transformation.
No Endogeneity
No endogeneity adalah adanya relasi antara independent variable dan error (error adalah perbedaan antara obrserved value dengan predicted value).
$Cov (x,\epsilon) = 0$
Masalah ini disebut Ommited Variable Bias. Hal ini terjadi ketika tidak memasukan relevant variables kedalam model.
- Variable y dipengaruhi oleh oleh var x1, Namun var x* juga mempengaruhi var y.
- Variable x* berkolerasi dengan x1, namun var x* tidak ada dalam perhitungan model.
- Semua yang tidak dapat dijelaskan oleh model, akan menjadi error.
- Akhirnya error menjadi berkolerasi dengan semua variable diatas.
Contoh: Model untuk prediksi harga apartemen di Jakarta. Tentu makin besar ukuran makin mahal harga apartemen. Namun model menunjukan sebaliknya, tentu ini tidak masuk akal.
Ketika model diperiksa, ternyata $Cov (x,\epsilon) \neq 0$ . Setelah dipelajari lebih dalam isi data. Ternyata ada data apartemen berlokasi di area CBD, walapun ukuran kecil namun harganya sangat mahal.
Karena variable lokasi ini tidak ada dalam perhitungan, model menjadi bias dalam melakukan predeksi.
Masalah ommited variable bias cukup sulit, karena itu pengalaman dan pengetahuan tentang latar belakang data yang diolah adalah penting. (Dalam contoh diatas, kita paham wilayah CBD adalah area super mahal).
Normality and homoscedasticity
- Normality, asumsi error term terdistribusi normal.
- Zero mean, jika mean bukan nol, maka garis regresi bukan regresi terbaik.
- Homoscedasticity, error term memiliki variance yang sama.
$\epsilon ~ N(0, \sigma^2)$
Jika error term tidak terdistribusi normal, gunakan Central Limit Theorem. Untuk sample yang besar, central limit theorem berlaku untuk error term. Jadi dapat kita asumsikan error term terdistribusi normal.
Error term zero mean, jika ekspektasi mean <> 0, maka garis regresi bukan yang terbaik. Penggunaan intercept dapat menyelesaikan masalah ini. Jadi dalam prakteknya, tidak akan ada masalah.
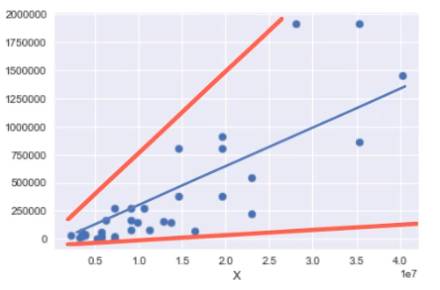
Homoscedasticity, jika variance pada error term tidak sama, maka garis regresi tidak akan baik. Lihat garis merah pada scater plot diatas. Regresi hanya menjelaskan pada independent dan dependent variable dengan value kecil.
Contoh dalam kehidupan nyata, Untuk kelompok kurang mampu, pengeluaran untuk makan tidak akan bervariasi terlalu besar secara value, kurang lebih pengeluaran untuk makan adalah 10-30 ribu per hari.
Sementara untuk kelompok mampu, pengeluaran untuk makan bisa sangat bervariatif, hari ini mungkin mereka makan-makan mewah di kafe-resto seperti steak kobe seharga 300rb, besoknya mungkin mereka tidak kemana-mana dan makan nasi goreng di rumah.
Dari contoh diatas, maka data pengeluaran termasuk heteroscedasticity. Untuk menghindari hal ini ada beberapa hal yang dapat dilakukan terhadap data.
- Cari Ommited Variable Bias.
- Hilangkan data outlier.
- Gunakan log transformation.
No Autocorellation
Disebut juga no serial corellation, covariance dari 2 error term adalah nol.
$\sigma_{\epsilon i \epsilon j} = 0$
Contoh dalam praktek sehari-hari adalah time series data seperti data stock market. Pada data stock market terjadi serial corellation pada error term. Untuk mendeteksi auto-corellation:
- Melihat pattern pada scatter plot
- Melihat durbin watson test dari OLS table, umumnya range nilai adalah 0 – 4. 2 menunjukan no-autocorellation, jika angka < 1 atau > 3 maka perlu perhatian.
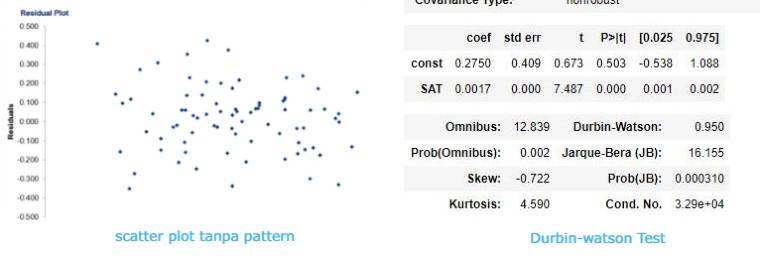
Jika ditemukan ada autocorellation, jangan gunakan linear regression, namun gunakan model regression lainnya seperti, autoregressive model, moving average model, autoregressive moving average model, autoregressive integrated moving average model.
No Multicollinearity
Adalah tidak ada kolerasi antara 2 atau lebih independent variable. Jika ada kolerasi, maka linear regression akan bermasalah, karena model akan salah melakukan perhitungan koefisien.
$\rho_{xiyj} \not\approx 1$
Contoh multicollinearity adalah seperti berikut. Jika A = 3 + 5 * B, maka kita bisa definisikan B = (A-3)/5. Pada persamaan ini disebut perfect multicollinearity atau $\rho_{xiyj} = 1$ .
Contoh dalam praktek, misalnya kita ingin market share black coffee dari kedai kopi setarbak vs meks. Untuk penyederhanaan, asumsi orang-orang hanya minum kopi diantara kedua kedai kopi ini. Jika harga disalah satu kedai lebih mahal, maka orang-orang akan berpindah ke kedai lainnya.
Untuk menghitung model, digunakan independent variable harga black coffe ukuran tall dan grande dari setarbak, dan harga black coffee ukuran reg dari meks.
Misal tall black coffee setarbak adalah 1000, dan grande adalah 1900. Untuk menarik pelanggan baru, maka dibuat harga baru. harga tall menjadi 900 dan harga grande menjadi 1700.
Saat melakukan perhitungan model, akan menjadi masalah, karena harga diatas berkolerasi satu sama lain. Karena harga black coffee tall dan grande bergerak bersamaan.
Untuk menghindari multicollinearity dapat dilakukan:
- Membuang salah satu variable
- Transform kedua variable tersebut menjadi satu variable